Goal

Right now, all I have is a simple quad being rendered with a texture. As I transition into doing more 3D stuff with this project, I want a way to move around my scene and see things. So this is what I'm going to be tackling next.

Idea

To get some sort of camera, we need to figure out how we're going to move around in 3D space. The two things we need to consider are translational and rotational movement.

In terms of, say an FPS, we can say that our translational movement is our WASD key movement, and the rotational movement is the mouse movement.

Translation is pretty easy. We just need to move our camera along some axis. To be more specific, what we actually need for our camera is an orthonormal basis. All this is just a set of three perpendicular unit vectors that define a coordinate system. Think X, Y, and Z axes.

What's most common is to define our camera coordinate frame with:

With these vectors, we can take our input, multiply it across the appropriate basis vector, and set our camera's position afterwards.

For rotation, we need to deal in angles. For me, I want to use a spherical coordinate system to define orientation. We need two angles:

Pitch and Yaw are also known as Polar and Azimuthal angles, respectively.

A diagram showing the spherical coordinate system (source: Wikipedia):

spherical coordinate system

Also, notice how I haven't mentioned Radial Distance yet. This is because we don't need it for and FPS-style camera (the kind I'm currently describing). We just need to know the direction the camera is facing, not how far it is from the origin. This will however become useful in an orbit camera controller, which I will also implement later.

What are we doing with these angles? Well, we need them to be able to calculate our camera's forward vector, which will lead us to getting the entire coordinate frame of our camera. We are defining our forward vector as the unit vector that points in the direction that the camera is facing. It's a direction vector, and none of these vectors have anything to do with position. This is where the distinction between points and vectors comes in, but that's not really the point of this so I won't really go into it.

Anyways, to do this we need to convert from spherical coordinates to cartesian coordinates.

This is the formula found on wikipedia:

spherical to cartesian

Ok, let's get into the details.

CameraController Class Implementation

For a proper camera controller class, we will need some things:

Here's what my CameraController class looks like:

class CameraController
{
protected:
    glm::vec3 m_pos;
    glm::vec3 m_forward, m_right, m_up;
    float m_pitch, m_yaw;
    float m_speed;
    float m_mouse_sensitivity;
    Input& m_input;

    void updateCameraVectors();

public:
    CameraController(Input& input, float speed, float sensitivity);
    virtual ~CameraController() = default;

    glm::mat4 getViewMatrix() const;

    const glm::vec3& getPosition() const { return m_pos; }
    const glm::vec3& getForward() const { return m_forward; }
    const glm::vec3& getRight() const { return m_right; }
    const glm::vec3& getUp() const { return m_up; }

    virtual void update(float delta_time) = 0;
};

Notice a few things here...

I have a custom Input class from a previous post that handles keyboard and mouse input already. I will just be using this to get input states.

The updateCameraVectors function is a protected member function that we will call in our update function if we need to (or possibly just every frame to be simple).

Big note here: The update function is pure virtual, making this an abstract class. This is because I want to make different types of camera controllers like I mentioned earlier (FPS, orbit, etc.) that will all inherit from this base class. Because of this, each type of camera controller will most likely need to implement their update logic differently. All of the other stuff is inherited though, which is nice. Being abstract also means we can't make instances of this class directly, only of derived classes.

Before we deal with all this virtual and abstract stuff, lets get the other member functions implemented.

Update Camera Vectors

Remember, our updateCameraVectors function will update our camera's coordinate frame based on our pitch and yaw angles.

Again, the goal is to calculate our forward, right, and up vectors to form our orthonormal basis so that we can move around in 3D space.

Recall the spherical to cartesian conversion formulas:

x = r * sin(θ) * cos(φ)
y = r * sin(θ) * sin(φ)
z = r * cos(θ)

I want to make a couple modifications to this actually.

Because this is an OpenGL project, I will be using a right-handed coordinate system, where:

To learn more about coordinate systems in a computer graphics context, I would check out this Scratchapixel article about coordinate systems, as well as their other articles. They are very good.

What this means for our camera's vectors, is that our forward vector will be pointing towards the negative Z axis when pitch and yaw are both zero.

Also, since we don't care about radial distance for now, we can just set r = 1.

With this in mind, and using our definitions of pitch (θ) and yaw (φ), we can rewrite the formulas as:

forward.x = cos(pitch) * sin(yaw);
forward.y = -sin(pitch);
forward.z = cos(pitch) * -cos(yaw);

Let's briefly explain why these are a bit different.

If you noticed, the y and z components are swapped! This is because the physics definition of spherical coordinates assumes a z-up system, but ours is y-up. So we just swap the y and z components to account for this.

Next, notice how the sines and cosines are sort of swapped (but not exactly)? This is because of how physics and game devs usually define their polar/pitch and azimuthal/yaw angles.

In physics, the polar angle is measured from the positive Z axis down towards the XY plane. In (usually) game dev however, pitch is usually measured from the XY plane up/down towards the Z axis in either direction. This means that when pitch is 0, we are looking straight ahead along the negative Z axis, and when pitch is 90 degrees, we are looking straight up along the positive Y axis.

Physics measures polar angle from the [0 <> 180] degree range, while game dev measures pitch from the [-90 <> 90] degree range.

θ = 0° -> looking straight up pitch = 0° -> looking straight ahead on horizontal plane

We can say that (θ = 90° - pitch).

If we substitute this into the physics formulas and use the trig cofunction identities, we get these substitutions for sin(θ) and cos(θ):

sin(θ) = sin(90° - pitch) = cos(pitch)
cos(θ) = cos(90° - pitch) = sin(pitch)

Similarly, with azimuthal/yaw angle, physics measures it from the positive X axis towards the positive Y axis in the XY plane. Game dev usually measures yaw from the negative Z axis towards the positive X axis in the XZ plane.

We can say that (φ = yaw - 90°).

Again, using the cofunction identities, we get these substitutions:

sin(φ) = sin(yaw - 90°) = -cos(yaw)
cos(φ) = cos(yaw - 90°) = sin(yaw)

Finally, I negate the y component of the forward vector because of how mouse delta is defined in my Input class. It is easier to negate it here, as opposed to negating mouse delta every time I read it.

And that's how we arrive at those formulas!

With the heavy math out of the way, here's how I implemented the updateCameraVectors function:

glm::vec3 CameraController::calculateForwardVector() const
{
    return glm::normalize(
        glm::vec3(cos(glm::radians(m_pitch)) * sin(glm::radians(m_yaw)),
                  -sin(glm::radians(m_pitch)),
                  cos(glm::radians(m_pitch)) * -cos(glm::radians(m_yaw))));
}

I'm using GLM here for the vector math.

Notice how we normalize the vector. This is important because we are not guaranteed a unit vector from the formulas above. It's easy to get confused and say that "each component is between -1 and 1, so the vector must be a unit vector", but that's not how that works. The length of the vector is determined by the square root of the sum of the squares of each component, which won't always be 1 here.

With the forward vector calculated, we can now easily get the up and right vectors using the cross product:

void CameraController::updateCameraVectors()
{
    m_forward = calculateForwardVector();

    // forward X world-up
    // world-up is always (0, 1, 0) in y-up convention
    m_right = glm::normalize(glm::cross(m_forward, glm::vec3(0.0f, 1.0f, 0.0f)));

    // right X forward
    m_up = glm::normalize(glm::cross(m_right, m_forward));
}

Because the cross product of two vectors results in a vector that is perpendicular to the plane formed by the two input vectors, we can form a basis with this.

Again, we normalize because the cross product does not guarantee a unit vector.

View Matrix

Previously, we would have just set our view matrix to a translation matrix based on the camera's position. Now, we need to account for rotation as well.

OpenGL provides us a cool function called glm::lookAt that does exactly what we need. It constructs a view matrix based on a camera position, a target position, and an up vector.

glm::mat4 CameraController::getViewMatrix() const
{
    return glm::lookAt(m_pos, m_pos + m_forward, m_up);
}

Here, our camera position is m_pos, our target position is m_pos + m_forward (a point in front of the camera), and our up vector is m_up.

That's pretty much it for the base CameraController class!

SpectatorCamera Class

Now, I'm going to implement our simple FPS-styled camera. I thought it would be better to call it a SpectatorCamera since it's not really tied to a player or any physical restrictions like being stuck on the ground.

This class will inherit from CameraController and pretty much just implement the update function.

Update Function

This is where all the input handling, movement, and rotation stuff will happen.

void SpectatorCamera::update(float delta_time)
{
    // handle keyboard input
    bool w_state = m_input.isKeyDown(GLFW_KEY_W);
    bool a_state = m_input.isKeyDown(GLFW_KEY_A);
    bool s_state = m_input.isKeyDown(GLFW_KEY_S);
    bool d_state = m_input.isKeyDown(GLFW_KEY_D);
    bool q_state = m_input.isKeyDown(GLFW_KEY_Q);
    bool e_state = m_input.isKeyDown(GLFW_KEY_E);

    glm::vec3 accumulated_input{0.0f};

    if (w_state)
        accumulated_input += m_forward;
    if (s_state)
        accumulated_input -= m_forward;
    if (a_state)
        accumulated_input -= m_right;
    if (d_state)
        accumulated_input += m_right;
    if (q_state)
        accumulated_input -= m_up;
    if (e_state)
        accumulated_input += m_up;

    if (glm::length(accumulated_input) > 0.0f)
    {
        accumulated_input = glm::normalize(accumulated_input);
        m_pos += m_speed * delta_time * accumulated_input;
    }

    // handle mouse input for looking
    glm::vec2 mouse_delta = m_input.getMouseDelta();
    mouse_delta *= m_mouse_sensitivity;

    m_yaw += mouse_delta.x;
    m_pitch += mouse_delta.y;

    // clamp pitch to prevent gimbal lock
    if (m_pitch > 89.0f)
    {
        m_pitch = 89.0f;
    }
    if (m_pitch < -89.0f)
    {
        m_pitch = -89.0f;
    }

    // update camera vectors if mouse moved
    if (mouse_delta.x != 0.0f || mouse_delta.y != 0.0f)
    {
        updateCameraVectors();
    }
}

Notice a few things here...

To get movement, we add/subtract the respective basis vectors to an accumulated_input vector based on key pressed. This is one reason we actually need those camera vectors.

We normalize the accumulated input vector before applying it to the position. This is so that diagonal movement isn't faster than straight movement which is a super common thing to do in games.

I also check if the length of the accumulated_input vector is greater than 0 before normalizing it. This is necessary so that we don't get a division by zero error when we normalize it.

Additionally, I clamp the pitch between -89 and 89 degrees to prevent gimbal lock. Gimbal lock happens when two of the three axes of rotation align, which causes you to lose one degree of freedom in rotation. By clamping pitch, we can avoid that case.

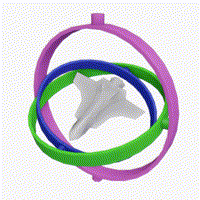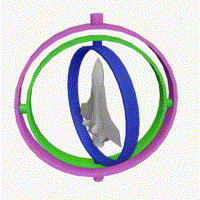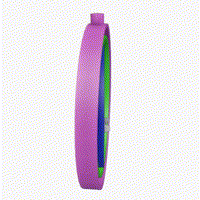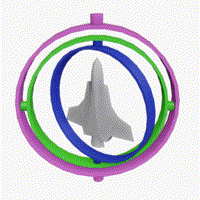
Wikipedia has a nice diagram showing gimbal lock: gimbal lock

Finally, we only call updateCameraVectors if there was mouse movement. This is an optimization to avoid unnecessary calculations when the camera orientation hasn't changed. I'm honestly not too sure how much of a performance gain this actually is, but it can't really hurt.

Conclusion

spectator camera demo

And that's pretty much it! I now have a functional camera controller system.

Next, I will be adding an orbit camera, asset loading, and some 3D models to render because what the heck is that gross pink quad?